How to calculate responsiveness in response to control using R?
In my previous post, I explained how to quantify phenotypic plasticity and introduced the concept of ‘responsiveness.’
□ Quantifying Phenotypic Plasticity of Crops
I introduced a formula to calculate responsiveness as (Treatment - Control) / Control.
| Genotype | Control | Treatment | Responsiveness |
| A | 100 | 90 | -10.0% |
| B | 120 | 70 | -41.7% |
| C | 115 | 90 | -21.7% |
| D | 95 | 85 | -10.5% |
| E | 110 | 105 | -4.5% |
However, when analyzing data, the format may not always be the same as above. Mostly, treatments (independent variable) are arranged in one column, and the dependent variable is arranged in another column. In this case, how to calculate responsiveness calculated as (Treatment - Control) / Control?
Let’s upload one data.
install.packages("readr")
library(readr)
github="https://raw.githubusercontent.com/agronomy4future/raw_data_practice/main/fertilizer_treatment.csv"
dataA= data.frame(read_csv(url(github),show_col_types = FALSE))
dataA
Genotype Block variable value
1 Genotype_A I Control 42.9
2 Genotype_A II Control 41.6
3 Genotype_A III Control 28.9
4 Genotype_A IV Control 30.8
5 Genotype_B I Control 53.3
6 Genotype_B II Control 69.6
7 Genotype_B III Control 45.4
8 Genotype_B IV Control 35.1
9 Genotype_C I Control 62.3
10 Genotype_C II Control 58.5
11 Genotype_C III Control 44.6
12 Genotype_C IV Control 50.3
13 Genotype_D I Control 75.4
14 Genotype_D II Control 65.6
15 Genotype_D III Control 54.0
16 Genotype_D IV Control 52.7
17 Genotype_A I Fertilizer1 53.8
18 Genotype_A II Fertilizer1 58.5
19 Genotype_A III Fertilizer1 43.9
20 Genotype_A IV Fertilizer1 46.3
21 Genotype_B I Fertilizer1 57.6
22 Genotype_B II Fertilizer1 69.6
23 Genotype_B III Fertilizer1 42.4
24 Genotype_B IV Fertilizer1 51.9
25 Genotype_C I Fertilizer1 63.4
26 Genotype_C II Fertilizer1 50.4
27 Genotype_C III Fertilizer1 45.0
28 Genotype_C IV Fertilizer1 46.7
29 Genotype_D I Fertilizer1 70.3
30 Genotype_D II Fertilizer1 67.3
31 Genotype_D III Fertilizer1 57.6
32 Genotype_D IV Fertilizer1 58.5
33 Genotype_A I Fertilizer2 49.5
34 Genotype_A II Fertilizer2 53.8
35 Genotype_A III Fertilizer2 40.7
36 Genotype_A IV Fertilizer2 39.4
37 Genotype_B I Fertilizer2 59.8
38 Genotype_B II Fertilizer2 65.8
39 Genotype_B III Fertilizer2 41.4
40 Genotype_B IV Fertilizer2 45.4
41 Genotype_C I Fertilizer2 64.5
42 Genotype_C II Fertilizer2 46.1
43 Genotype_C III Fertilizer2 62.6
44 Genotype_C IV Fertilizer2 50.3
45 Genotype_D I Fertilizer2 68.8
46 Genotype_D II Fertilizer2 65.3
47 Genotype_D III Fertilizer2 45.6
48 Genotype_D IV Fertilizer2 51.0
49 Genotype_A I Fertilizer3 44.4
50 Genotype_A II Fertilizer3 41.8
51 Genotype_A III Fertilizer3 28.3
52 Genotype_A IV Fertilizer3 34.7
53 Genotype_B I Fertilizer3 64.1
54 Genotype_B II Fertilizer3 57.4
55 Genotype_B III Fertilizer3 44.1
56 Genotype_B IV Fertilizer3 51.6
57 Genotype_C I Fertilizer3 63.6
58 Genotype_C II Fertilizer3 56.1
59 Genotype_C III Fertilizer3 52.7
60 Genotype_C IV Fertilizer3 51.8
61 Genotype_D I Fertilizer3 71.6
62 Genotype_D II Fertilizer3 69.4
63 Genotype_D III Fertilizer3 56.6
64 Genotype_D IV Fertilizer3 47.4This data has two treatments (independent variables) with 4 replicates.
xtabs(~variable + Genotype, data=dataA)
Genotype
variable Genotype_A Genotype_B Genotype_C Genotype_D
Control 4 4 4 4
Fertilizer1 4 4 4 4
Fertilizer2 4 4 4 4
Fertilizer3 4 4 4 4Now, I’ll calculate the ‘responsiveness’ of yield for each fertilizer in response to control.
library(dplyr)
dataA=data.frame(dataA %>%
group_by(Genotype) %>%
mutate(responsiveness=ifelse(variable!="Control",
(value-value[variable=="Control"])/value[variable=="Control"], NA)))
dataA
Genotype Block variable value responsiveness
1 Genotype_A I Control 42.9 NA
2 Genotype_A II Control 41.6 NA
3 Genotype_A III Control 28.9 NA
4 Genotype_A IV Control 30.8 NA
5 Genotype_B I Control 53.3 NA
6 Genotype_B II Control 69.6 NA
7 Genotype_B III Control 45.4 NA
8 Genotype_B IV Control 35.1 NA
9 Genotype_C I Control 62.3 NA
10 Genotype_C II Control 58.5 NA
11 Genotype_C III Control 44.6 NA
12 Genotype_C IV Control 50.3 NA
13 Genotype_D I Control 75.4 NA
14 Genotype_D II Control 65.6 NA
15 Genotype_D III Control 54.0 NA
16 Genotype_D IV Control 52.7 NA
17 Genotype_A I Fertilizer1 53.8 0.254079254
18 Genotype_A II Fertilizer1 58.5 0.406250000
19 Genotype_A III Fertilizer1 43.9 0.519031142
20 Genotype_A IV Fertilizer1 46.3 0.503246753
21 Genotype_B I Fertilizer1 57.6 0.080675422
22 Genotype_B II Fertilizer1 69.6 0.000000000
23 Genotype_B III Fertilizer1 42.4 -0.066079295
24 Genotype_B IV Fertilizer1 51.9 0.478632479
25 Genotype_C I Fertilizer1 63.4 0.017656501
26 Genotype_C II Fertilizer1 50.4 -0.138461538
27 Genotype_C III Fertilizer1 45.0 0.008968610
28 Genotype_C IV Fertilizer1 46.7 -0.071570577
29 Genotype_D I Fertilizer1 70.3 -0.067639257
30 Genotype_D II Fertilizer1 67.3 0.025914634
31 Genotype_D III Fertilizer1 57.6 0.066666667
32 Genotype_D IV Fertilizer1 58.5 0.110056926
33 Genotype_A I Fertilizer2 49.5 0.153846154
34 Genotype_A II Fertilizer2 53.8 0.293269231
35 Genotype_A III Fertilizer2 40.7 0.408304498
36 Genotype_A IV Fertilizer2 39.4 0.279220779
37 Genotype_B I Fertilizer2 59.8 0.121951220
38 Genotype_B II Fertilizer2 65.8 -0.054597701
39 Genotype_B III Fertilizer2 41.4 -0.088105727
40 Genotype_B IV Fertilizer2 45.4 0.293447293
41 Genotype_C I Fertilizer2 64.5 0.035313002
42 Genotype_C II Fertilizer2 46.1 -0.211965812
43 Genotype_C III Fertilizer2 62.6 0.403587444
44 Genotype_C IV Fertilizer2 50.3 0.000000000
45 Genotype_D I Fertilizer2 68.8 -0.087533156
46 Genotype_D II Fertilizer2 65.3 -0.004573171
47 Genotype_D III Fertilizer2 45.6 -0.155555556
48 Genotype_D IV Fertilizer2 51.0 -0.032258065
49 Genotype_A I Fertilizer3 44.4 0.034965035
50 Genotype_A II Fertilizer3 41.8 0.004807692
51 Genotype_A III Fertilizer3 28.3 -0.020761246
52 Genotype_A IV Fertilizer3 34.7 0.126623377
53 Genotype_B I Fertilizer3 64.1 0.202626642
54 Genotype_B II Fertilizer3 57.4 -0.175287356
55 Genotype_B III Fertilizer3 44.1 -0.028634361
56 Genotype_B IV Fertilizer3 51.6 0.470085470
57 Genotype_C I Fertilizer3 63.6 0.020866774
58 Genotype_C II Fertilizer3 56.1 -0.041025641
59 Genotype_C III Fertilizer3 52.7 0.181614350
60 Genotype_C IV Fertilizer3 51.8 0.029821074
61 Genotype_D I Fertilizer3 71.6 -0.050397878
62 Genotype_D II Fertilizer3 69.4 0.057926829
63 Genotype_D III Fertilizer3 56.6 0.048148148
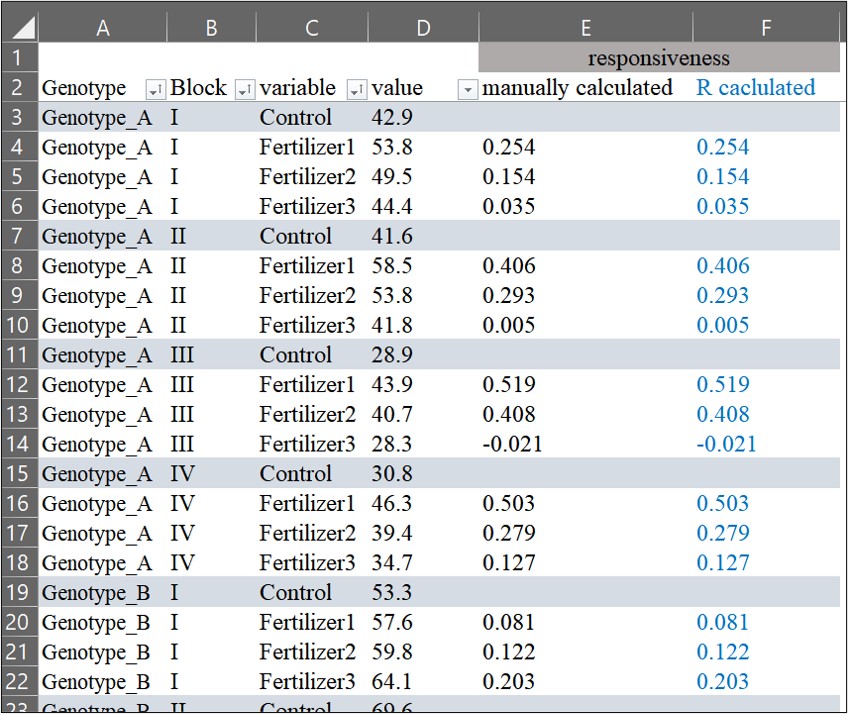
64 Genotype_D IV Fertilizer3 47.4 -0.100569260I’ll check if this calculation is correct. Let’s download this data as an Excel file.
#install.packages("writexl")
library(writexl)
write_xlsx (dataA,"C:/Users/Desktop/dataA.xlsx")Then, I compared what I calculated manually with what R calculated, and they are the same.
How to calculate when several groups exist?
The previous data only includes replicates from a single group (genotype). My next question is how to calculate when multiple groups are present?
This dataset involves different planting rows, including outside, east, west, and middle divisions. It analyzes biomass yield per wheat head and stem in response to three conditions: control, tr1, and tr2. How should I calculate responsiveness for each group combination in this scenario? I already calculated responsiveness using excel.
library(readr)
github="https://raw.githubusercontent.com/agronomy4future/raw_data_practice/main/responsiveness.csv"
dataA= data.frame(read_csv(url(github),show_col_types = FALSE))
dataA
tissue row plot treatment yield responsiveness
1 Head outside 5 Control 159.30 <NA>
2 Head outside 5 Tr1 59.70 -62.5%
3 Head outside 5 Tr2 97.50 -38.8%
4 Stem outside 5 Control 74.65 <NA>
5 Stem outside 5 Tr1 34.05 -54.4%
6 Stem outside 5 Tr2 76.65 2.7%
7 Head outside 6 Control 99.30 <NA>
8 Head outside 6 Tr1 109.00 9.8%
9 Head outside 6 Tr2 82.30 -17.1%
10 Stem outside 6 Control 53.95 <NA>
11 Stem outside 6 Tr1 52.95 -1.9%
12 Stem outside 6 Tr2 65.45 21.3%
.
.
.Now I’ll calculate the responsiveness using R by groups.
library(dplyr)
dataB=data.frame(dataA %>%
group_by(tissue, row, plot) %>%
mutate(Calculation=ifelse(treatment!="Control",
(yield-yield[treatment=="Control"])/yield[treatment=="Control"], NA)))
dataB
tissue row plot treatment yield responsiveness Calculation
1 Head outside 5 Control 159.30 <NA> NA
2 Head outside 5 Tr1 59.70 -62.5% -0.200267917
3 Head outside 5 Tr2 97.50 -38.8% -0.018126888
4 Stem outside 5 Control 74.65 <NA> NA
5 Stem outside 5 Tr1 34.05 -54.4% -0.714824121
6 Stem outside 5 Tr2 76.65 2.7% 0.243309002
7 Head outside 6 Control 99.30 <NA> NA
8 Head outside 6 Tr1 109.00 9.8% 0.405544810
9 Head outside 6 Tr2 82.30 -17.1% 0.567619048
10 Stem outside 6 Control 53.95 <NA> NA
11 Stem outside 6 Tr1 52.95 -1.9% -0.278610354
12 Stem outside 6 Tr2 65.45 21.3% 0.348094748
.
.
.However, as you can see, the calculated value differs from what I calculated using excel This issue can occur when the ‘plyr’ package is installed. To resolve it, you can either uninstall the ‘plyr’ package or use the dplyr::mutate function.
dataB=data.frame(dataA %>%
group_by(tissue, row, plot) %>%
dplyr::mutate(Calculation=ifelse(treatment!="Control",
(yield-yield[treatment=="Control"])/yield[treatment=="Control"], NA)))
dataB
tissue row plot treatment yield responsiveness Calculation
1 Head outside 5 Control 159.30 <NA> NA
2 Head outside 5 Tr1 59.70 -62.5% -0.62523540
3 Head outside 5 Tr2 97.50 -38.8% -0.38794727
4 Stem outside 5 Control 74.65 <NA> NA
5 Stem outside 5 Tr1 34.05 -54.4% -0.54387140
6 Stem outside 5 Tr2 76.65 2.7% 0.02679169
7 Head outside 6 Control 99.30 <NA> NA
8 Head outside 6 Tr1 109.00 9.8% 0.09768379
9 Head outside 6 Tr2 82.30 -17.1% -0.17119839
10 Stem outside 6 Control 53.95 <NA> NA
11 Stem outside 6 Tr1 52.95 -1.9% -0.01853568
12 Stem outside 6 Tr2 65.45 21.3% 0.21316033Now, the value will be the same.
How about calculating responsiveness using the mean?
Next, I want to determine responsiveness by averaging the yield. Therefore, the first step is to calculate the average yield.
library (plyr)
dataC=ddply(dataA, c("tissue","row","treatment"), summarise, mean=mean(yield))
colnames(dataC)[4]=c("yield")
dataC
tissue row treatment yield
1 Head east Control 71.8000
2 Head east Tr1 52.7375
3 Head east Tr2 45.1750
4 Head middle Control 62.9000
5 Head middle Tr1 57.8250
6 Head middle Tr2 37.2250
7 Head outside Control 118.0500
8 Head outside Tr1 137.6500
9 Head outside Tr2 96.8250
10 Head west Control 73.8750
11 Head west Tr1 60.9125
12 Head west Tr2 47.6000
13 Stem east Control 48.5500
14 Stem east Tr1 35.1875
15 Stem east Tr2 53.9375
16 Stem middle Control 41.3750
17 Stem middle Tr1 36.3750
18 Stem middle Tr2 63.6250
19 Stem outside Control 66.9500
20 Stem outside Tr1 71.7750
21 Stem outside Tr2 79.1000
22 Stem west Control 50.6250
23 Stem west Tr1 38.1500
24 Stem west Tr2 55.2250Then, I’ll calculate responsiveness again.
library(dplyr)
dataD=data.frame(dataC %>%
group_by(tissue, row) %>%
dplyr::mutate(responsiveness=ifelse(treatment!="Control",
(yield-yield[treatment=="Control"])/yield[treatment=="Control"], NA)))
dataD
tissue row treatment yield responsiveness
1 Head east Control 71.8000 NA
2 Head east Tr1 52.7375 -0.26549443
3 Head east Tr2 45.1750 -0.37082173
4 Head middle Control 62.9000 NA
5 Head middle Tr1 57.8250 -0.08068362
6 Head middle Tr2 37.2250 -0.40818760
7 Head outside Control 118.0500 NA
8 Head outside Tr1 137.6500 0.16603134
9 Head outside Tr2 96.8250 -0.17979670
10 Head west Control 73.8750 NA
11 Head west Tr1 60.9125 -0.17546531
12 Head west Tr2 47.6000 -0.35566836
13 Stem east Control 48.5500 NA
14 Stem east Tr1 35.1875 -0.27523172
15 Stem east Tr2 53.9375 0.11096807
16 Stem middle Control 41.3750 NA
17 Stem middle Tr1 36.3750 -0.12084592
18 Stem middle Tr2 63.6250 0.53776435
19 Stem outside Control 66.9500 NA
20 Stem outside Tr1 71.7750 0.07206871
21 Stem outside Tr2 79.1000 0.18147872
22 Stem west Control 50.6250 NA
23 Stem west Tr1 38.1500 -0.24641975
24 Stem west Tr2 55.2250 0.09086420Tip!! How about we consider reshaping the data format??
Let’s go back to dataA. After going through the above process to calculate responsiveness due to variables being in the same column, how about we reshape the data format to facilitate the calculation of responsiveness more easily?
dataA
Genotype Block variable value
1 Genotype_A I Control 42.9
2 Genotype_A II Control 41.6
3 Genotype_A III Control 28.9
4 Genotype_A IV Control 30.8
5 Genotype_B I Control 53.3
6 Genotype_B II Control 69.6
7 Genotype_B III Control 45.4
8 Genotype_B IV Control 35.1
9 Genotype_C I Control 62.3
10 Genotype_C II Control 58.5
.
.
.Let’s use the below code to reshape data format.
library(dplyr)
library(tidyr)
dataB= data.frame(dataA %>%
group_by(Genotype, Block, variable) %>%
spread(key=variable, value=value))
dataB
Genotype Block Control Fertilizer1 Fertilizer2 Fertilizer3
1 Genotype_A I 42.9 53.8 49.5 44.4
2 Genotype_A II 41.6 58.5 53.8 41.8
3 Genotype_A III 28.9 43.9 40.7 28.3
4 Genotype_A IV 30.8 46.3 39.4 34.7
5 Genotype_B I 53.3 57.6 59.8 64.1
6 Genotype_B II 69.6 69.6 65.8 57.4
7 Genotype_B III 45.4 42.4 41.4 44.1
8 Genotype_B IV 35.1 51.9 45.4 51.6
9 Genotype_C I 62.3 63.4 64.5 63.6
10 Genotype_C II 58.5 50.4 46.1 56.1
11 Genotype_C III 44.6 45.0 62.6 52.7
12 Genotype_C IV 50.3 46.7 50.3 51.8
13 Genotype_D I 75.4 70.3 68.8 71.6
14 Genotype_D II 65.6 67.3 65.3 69.4
15 Genotype_D III 54.0 57.6 45.6 56.6
16 Genotype_D IV 52.7 58.5 51.0 47.4Then we can easily calculate the responsiveness.
dataB$R_Fertilizer1=(dataB$Fertilizer1-dataB$Control)/dataB$Control
dataB$R_Fertilizer2=(dataB$Fertilizer2-dataB$Control)/dataB$Control
dataB$R_Fertilizer3=(dataB$Fertilizer2-dataB$Control)/dataB$Control
dataB
Genotype Block Control Fertilizer1 Fertilizer2 Fertilizer3 R_Fertilizer1 R_Fertilizer2 R_Fertilizer3
1 Genotype_A I 42.9 53.8 49.5 44.4 0.25407925 0.153846154 0.153846154
2 Genotype_A II 41.6 58.5 53.8 41.8 0.40625000 0.293269231 0.293269231
3 Genotype_A III 28.9 43.9 40.7 28.3 0.51903114 0.408304498 0.408304498
4 Genotype_A IV 30.8 46.3 39.4 34.7 0.50324675 0.279220779 0.279220779
5 Genotype_B I 53.3 57.6 59.8 64.1 0.08067542 0.121951220 0.121951220
6 Genotype_B II 69.6 69.6 65.8 57.4 0.00000000 -0.054597701 -0.054597701
7 Genotype_B III 45.4 42.4 41.4 44.1 -0.06607930 -0.088105727 -0.088105727
8 Genotype_B IV 35.1 51.9 45.4 51.6 0.47863248 0.293447293 0.293447293
9 Genotype_C I 62.3 63.4 64.5 63.6 0.01765650 0.035313002 0.035313002
10 Genotype_C II 58.5 50.4 46.1 56.1 -0.13846154 -0.211965812 -0.211965812
11 Genotype_C III 44.6 45.0 62.6 52.7 0.00896861 0.403587444 0.403587444
12 Genotype_C IV 50.3 46.7 50.3 51.8 -0.07157058 0.000000000 0.000000000
13 Genotype_D I 75.4 70.3 68.8 71.6 -0.06763926 -0.087533156 -0.087533156
14 Genotype_D II 65.6 67.3 65.3 69.4 0.02591463 -0.004573171 -0.004573171
15 Genotype_D III 54.0 57.6 45.6 56.6 0.06666667 -0.155555556 -0.155555556
16 Genotype_D IV 52.7 58.5 51.0 47.4 0.11005693 -0.032258065 -0.032258065Then, let’s reshape data again.
dataC= data.frame(pivot_longer(dataB,
cols= starts_with("R_Fertilizer"),
names_to= "Responsiveness",
values_to= "Value"))
dataC
Genotype Block Control Fertilizer1 Fertilizer2 Fertilizer3 Responsiveness Value
1 Genotype_A I 42.9 53.8 49.5 44.4 R_Fertilizer1 0.254079254
2 Genotype_A I 42.9 53.8 49.5 44.4 R_Fertilizer2 0.153846154
3 Genotype_A I 42.9 53.8 49.5 44.4 R_Fertilizer3 0.153846154
4 Genotype_A II 41.6 58.5 53.8 41.8 R_Fertilizer1 0.406250000
5 Genotype_A II 41.6 58.5 53.8 41.8 R_Fertilizer2 0.293269231
6 Genotype_A II 41.6 58.5 53.8 41.8 R_Fertilizer3 0.293269231
7 Genotype_A III 28.9 43.9 40.7 28.3 R_Fertilizer1 0.519031142
8 Genotype_A III 28.9 43.9 40.7 28.3 R_Fertilizer2 0.408304498
9 Genotype_A III 28.9 43.9 40.7 28.3 R_Fertilizer3 0.408304498
10 Genotype_A IV 30.8 46.3 39.4 34.7 R_Fertilizer1 0.503246753