Exploring Best Linear Unbiased Estimators (BLUE) through Practical Examples in R
□ The Best Linear Unbiased Estimator (BLUE): Step-by-Step Guide using R (with AllInOne Package)
In my previous post, I explained how to use R to perform the Best Linear Unbiased Estimator (BLUE). Now, this is a practical exercise focusing on BLUE in R.
Here is one dataset.
library(readr)
github="https://raw.githubusercontent.com/agronomy4future/raw_data_practice/main/genotype_transgenic_line_with_fertilizer.csv"
dataA= data.frame(read_csv(url(github), show_col_types= FALSE))
dataA
genotype plot resistance fertilizer GN AGW
1 cv1 1 no 150 1310 33.15
2 cv1 1 no 0 1168 25.07
3 cv1 1 no 200 570 36.04
4 cv2 1 no 150 1120 53.05
5 cv2 1 no 0 1230 26.71
6 cv2 1 no 200 795 37.75
7 cv3 1 yes 150 2013 27.51
8 cv3 1 yes 0 2183 24.61
9 cv3 1 yes 200 1034 36.53
10 cv4 1 no 150 2451 31.58
.
.
.I have data on grain number (GN) and average grain weight (AGW) in winter wheat for about five genotypes and one transgenic line. The study examines the response to disease resistance (yes or no) and fertilizer application at three levels 0 kg N ha-1, 150 kg N ha-1 and 200 kg N ha-1).
First, let’s summarize data.
library(dplyr)
dataB = data.frame(dataA %>%
group_by(genotype, resistance, fertilizer) %>%
dplyr::summarize(across(c(GN, AGW),
.fns= list(Mean=~mean(., na.rm= TRUE),
SD= ~sd(., na.rm= TRUE),
n=~length(.),
se=~sd(.,na.rm= TRUE) / sqrt(length(.))))))
dataB= dataB[,-c(5,6,9,10)]
dataB
genotype resistance fertilizer GN_Mean GN_se AGW_Mean AGW_se
1 Transgeic_line yes 0 2872.50 268.22643 25.2850 1.7322360
2 Transgeic_line yes 150 3895.50 351.74956 27.7825 1.8239032
3 Transgeic_line yes 200 2285.50 58.41589 34.8625 1.8272902
4 cv1 no 0 1802.25 229.84320 25.1050 1.1437111
5 cv1 no 150 1902.25 215.03696 31.4900 0.5558327
6 cv1 no 200 1050.25 168.08647 37.3550 0.9006803
7 cv2 no 0 1529.00 152.99782 24.4525 1.1642907
8 cv2 no 150 1752.50 262.66408 35.0600 6.0786388
9 cv2 no 200 951.50 143.49826 36.0025 1.4648457
10 cv3 yes 0 2064.00 85.79141 21.1175 1.4288887
11 cv3 yes 150 1968.50 112.31615 25.4075 1.0330568
12 cv3 yes 200 812.25 263.48257 36.6200 0.9226682
13 cv4 no 0 2391.00 289.96207 24.6600 0.5913967
14 cv4 no 150 2082.25 153.83832 30.1225 0.9788971
15 cv4 no 200 1277.00 164.44807 33.8650 0.9269799
16 cv5 no 0 1593.00 153.43294 23.2125 0.7888745
17 cv5 no 150 1875.25 92.15148 30.3475 0.7051285
18 cv5 no 200 975.75 50.51629 34.9950 1.0727263Then, I’ll create a graph, but before creating a graph, let’s rename some variables.
library (stringr)
dataB$genotype= str_replace_all (dataB$genotype, 'Transgeic_line','TL')
dataB$fertilizer <- str_replace_all(dataB$fertilizer, '\\b0\\b', '0 kg/ha')
dataB$fertilizer= str_replace_all (dataB$fertilizer, '150','150 kg/ha')
dataB$fertilizer= str_replace_all (dataB$fertilizer, '200','200 kg/ha')and let’s create a graph.
FIG1=ggplot(data=dataB, aes(x=genotype, y=GN_Mean, fill=resistance))+
geom_bar(stat="identity",position="dodge", width= 0.7, size=1) +
scale_fill_manual(values=c("grey75","cadetblue"))+
geom_errorbar(aes(ymin=GN_Mean-GN_se, ymax=GN_Mean+GN_se),
position=position_dodge(0.9), width=0.5) +
scale_y_continuous(breaks=seq(0,5000,1000), limits = c(0,5000)) +
facet_wrap (~ fertilizer, scales="free_y") +
labs(x="Genotype", y="Grain number") +
theme_classic(base_size=18, base_family="serif")+
theme(legend.position="bottom",
legend.title=element_text(family="serif", face="plain",
size=13, color= "Black"),
legend.key=element_rect(color="white", fill="white"),
legend.text=element_text(family="serif", face="plain",
size=13, color= "Black"),
legend.background=element_rect(fill="white"),
axis.line=element_line(linewidth=0.5, colour="black"),
strip.background=element_rect(color="white",
linewidth=0.5, linetype="solid"))
FIG1 + windows (width=12, height=5)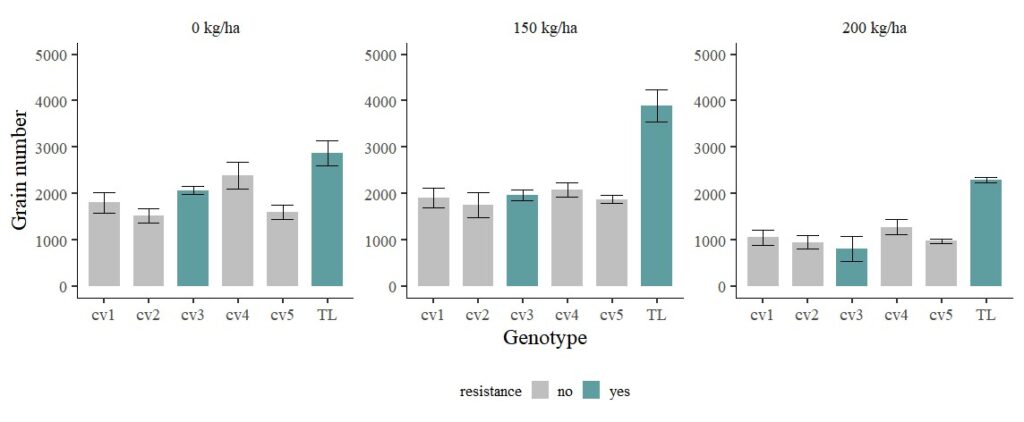
Now, transgenic line (TL) shows much greater grain number. I’ll exclude transgenic line (TL).
FIG1=ggplot(data=subset(dataB, genotype!="TL"), aes(x=genotype, y=GN_Mean, fill=resistance))+
geom_bar(stat="identity",position="dodge", width= 0.7, size=1) +
scale_fill_manual(values=c("grey75","cadetblue"))+
geom_errorbar(aes(ymin=GN_Mean-GN_se, ymax=GN_Mean+GN_se),
position=position_dodge(0.9), width=0.5) +
scale_y_continuous(breaks=seq(0,3500,500), limits = c(0,3500)) +
facet_wrap (~ fertilizer, scales="free_y") +
labs(x="Genotype", y="Grain number") +
theme_classic(base_size=18, base_family="serif")+
theme(legend.position="bottom",
legend.title=element_text(family="serif", face="plain",
size=13, color= "Black"),
legend.key=element_rect(color="white", fill="white"),
legend.text=element_text(family="serif", face="plain",
size=13, color= "Black"),
legend.background=element_rect(fill="white"),
axis.line=element_line(linewidth=0.5, colour="black"),
strip.background=element_rect(color="white",
linewidth=0.5,linetype="solid"))
FIG1 + windows (width=12, height=5)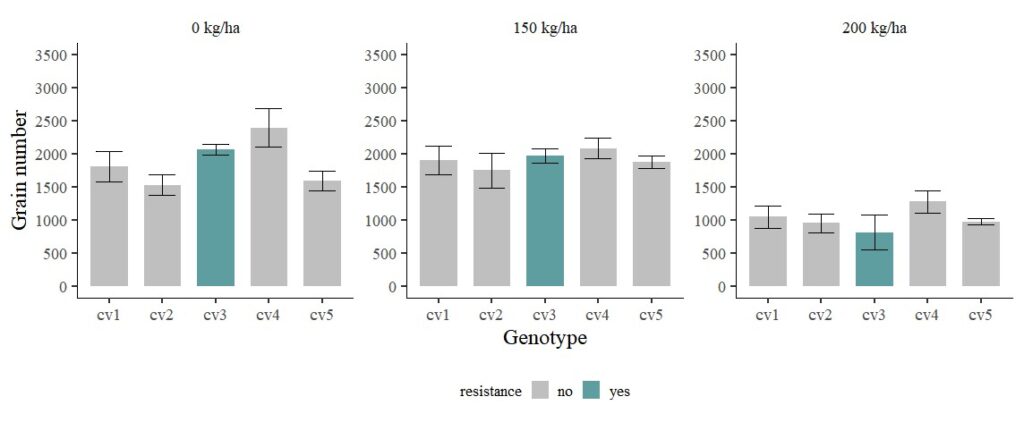
When running statistical analyses, only 0 kg/ha shows significant differences among genotypes, while there is no difference under both 150 kg/ha and 200 kg/ha. While the observed mean values appear distinct, the presence of a substantial standard error, indicative of significant data variability, leads to a situation where the statistical analysis fails to detect a significant difference in means.
In statistical terms, the standard error is a measure of how much the sample mean is expected to vary from the true population mean. When the standard error is large, it means that there is a considerable amount of variability in the data, making it more challenging to detect a true difference in means. If the standard error is large, it may result in a larger standard deviation of the sample mean and a wider confidence interval, which in turn can lead to a p-value that is not significant. It’s essential to consider both the mean difference and the standard error when interpreting statistical results. If the standard error is large, it may indicate that the observed mean difference is not likely to be statistically significant. In such cases, researchers might focus on understanding and interpreting the variability in the data and consider collecting more data to reduce the standard error and improve the precision of the estimates.
To address the challenge posed by high data variability and the resulting lack of statistical significance in mean differences, one effective approach is to employ the Best Linear Unbiased Estimator (BLUE) or Best Linear Unbiased Predictor (BLUP). These methods offer a robust means of adjusting for errors in statistical estimates. BLUE and BLUP take into account both the mean differences and the underlying variability, providing more stable and unbiased estimates, especially in situations where data variability is pronounced. By incorporating these estimators, researchers can obtain more reliable and precise insights, enhancing the interpretability and robustness of their statistical analyses.
□ The Best Linear Unbiased Estimator (BLUE): Step-by-Step Guide using R (with AllInOne Package)
I’ll use this code.
library(lme4)
library(Matrix)
dataA= subset(dataA, genotype!="Transgeic_line")
BLUE_0_kg_ha=lmer(GN ~ 0 + (1|genotype), data=subset(dataA, fertilizer=="0"))
BLUE_150_kg_ha=lmer(GN ~ 0 + (1|genotype), data=subset(dataA, fertilizer=="150"))
BLUE_200_kg_ha=lmer(GN ~ 0 + (1|genotype), data=subset(dataA, fertilizer=="200"))In the provided code, I formulated distinct linear mixed-effects models within each fertilizer treatment using lmer(GN ~ 0 + (1|genotype) for “0,” “150,” and “200” kg/ha treatments. In each instance, I established a fixed intercept (0) and incorporated a random intercept for the variable genotype. The designation “Best Linear Unbiased Estimator (BLUE)” commonly refers to the fixed effects within the context of linear mixed-effects models. Here, the fixed intercept term in each model operates as a manifestation of BLUE, representing an estimate that minimizes the sum of squared differences between predicted and observed values.
To provide a bit more context:
- Best: The fixed effects are chosen to minimize the sum of squared differences between the predicted values and the observed values.
- Linear: The model is linear in terms of parameters, meaning it is a linear combination of the predictor variables and their coefficients.
- Unbiased: The estimates are unbiased, meaning on average, they are equal to the true values in the population.
- Estimator: This refers to the coefficients (fixed effects) in the model.
It is crucial to note that the (1|genotype) term introduces a random intercept for the variable genotype, allowing for variability in intercepts across different levels of the genotype variable. This incorporation of a random effect aligns with the broader framework of estimating best linear unbiased predictors (BLUPs) within a mixed-effects model. The utilization of these models is particularly valuable for addressing data variability and deriving unbiased estimates of fixed effects tailored to each fertilizer treatment.
The next step is to integrate the predicted values generated by the Best Linear Unbiased Estimators (BLUE) into the original dataset. To commence this procedure, we first calculate these predicted values.
BLUE_0= predict (BLUE_0_kg_ha)
BLUE_150= predict (BLUE_150_kg_ha)
BLUE_200=predict (BLUE_200_kg_ha)This step holds particular importance, signifying that when considering genotype as a random effect, the estimations encapsulate values strategically chosen to minimize the collective sum of squared differences between the expected and observed values. This refined adjustment facilitates a more nuanced comprehension of the inherent variability in the data, thereby elevating the precision and reliability of our statistical estimates.
Let’s add each predicted values to the original data set.
dataA$predicted_0 <- NA
dataA$predicted_0[dataA$fertilizer==0] <- BLUE_0
dataA$predicted_150 <- NA
dataA$predicted_150[dataA$fertilizer==150] <- BLUE_150
dataA$predicted_200 <- NA
dataA$predicted_200[dataA$fertilizer==200] <- BLUE_200
library(dplyr)
dataB= dataA %>%
mutate(BLUE_GN= coalesce(predicted_0, predicted_150, predicted_200))
dataB= dataB[,-c(7,8,9)]
dataB
genotype plot resistance fertilizer GN AGW BLUE_GN
1 cv1 1 no 150 1310 33.15 1885.7234
2 cv1 1 no 0 1168 25.07 1783.2109
3 cv1 1 no 200 570 36.04 1020.6757
4 cv2 1 no 150 1120 53.05 1737.2744
5 cv2 1 no 0 1230 26.71 1512.8475
6 cv2 1 no 200 795 37.75 924.7064
7 cv3 1 yes 150 2013 27.51 1951.3979
8 cv3 1 yes 0 2183 24.61 2042.1957
9 cv3 1 yes 200 1034 36.53 789.3776
10 cv4 1 no 150 2451 31.58 2064.1596
.
.
.Now I have added the predicted values to the original dataset. Let’s summarize the data.
library(dplyr)
dataC = data.frame(dataB %>%
group_by(genotype, resistance, fertilizer) %>%
dplyr::summarize(across(c(GN, BLUE_GN),
.fns= list(Mean=~mean(., na.rm= TRUE),
SD= ~sd(., na.rm= TRUE),
n=~length(.),
se=~sd(.,na.rm= TRUE)/sqrt(length(.))))))
dataC= dataC[,-c(5,6,9,10)]
dataC
genotype resistance fertilizer GN_Mean GN_se BLUE_GN_Mean BLUE_GN_se
1 cv1 no 0 1802.25 229.84320 1783.2109 0
2 cv1 no 150 1902.25 215.03696 1885.7234 0
3 cv1 no 200 1050.25 168.08647 1020.6757 0
4 cv2 no 0 1529.00 152.99782 1512.8475 0
5 cv2 no 150 1752.50 262.66408 1737.2744 0
6 cv2 no 200 951.50 143.49826 924.7064 0
7 cv3 yes 0 2064.00 85.79141 2042.1957 0
8 cv3 yes 150 1968.50 112.31615 1951.3979 0
9 cv3 yes 200 812.25 263.48257 789.3776 0
10 cv4 no 0 2391.00 289.96207 2365.7413 0
.
.
.library (stringr)
dataC$fertilizer= str_replace_all(dataC$fertilizer, '\\b0\\b', '0 kg/ha')
dataC$fertilizer= str_replace_all (dataC$fertilizer, '150','150 kg/ha')
dataC$fertilizer= str_replace_all (dataC$fertilizer, '200','200 kg/ha')
library (ggplot2)
FIG1=ggplot(data=dataC, aes(x=genotype, y=BLUE_GN_Mean, fill=resistance))+
geom_bar(stat="identity",position="dodge", width= 0.7, size=1) +
scale_fill_manual(values=c("grey75","cadetblue"))+
geom_errorbar(aes(ymin=BLUE_GN_Mean-BLUE_GN_se, ymax=BLUE_GN_Mean+BLUE_GN_se),
position=position_dodge(0.9), width=0.5) +
scale_y_continuous(breaks=seq(0,3500,500), limits = c(0,3500)) +
facet_wrap (~ fertilizer, scales="free_y") +
labs(x="Genotype", y="Grain number") +
theme_classic(base_size=18, base_family="serif")+
theme(legend.position="bottom",
legend.title=element_text(family="serif", face="plain",
size=13, color= "Black"),
legend.key=element_rect(color="white", fill="white"),
legend.text=element_text(family="serif", face="plain",
size=13, color= "Black"),
legend.background=element_rect(fill="white"),
axis.line=element_line(linewidth=0.5, colour="black"),
strip.background=element_rect(color="white",
linewidth=0.5,linetype="solid"))
FIG1 + windows(width=12, height=5)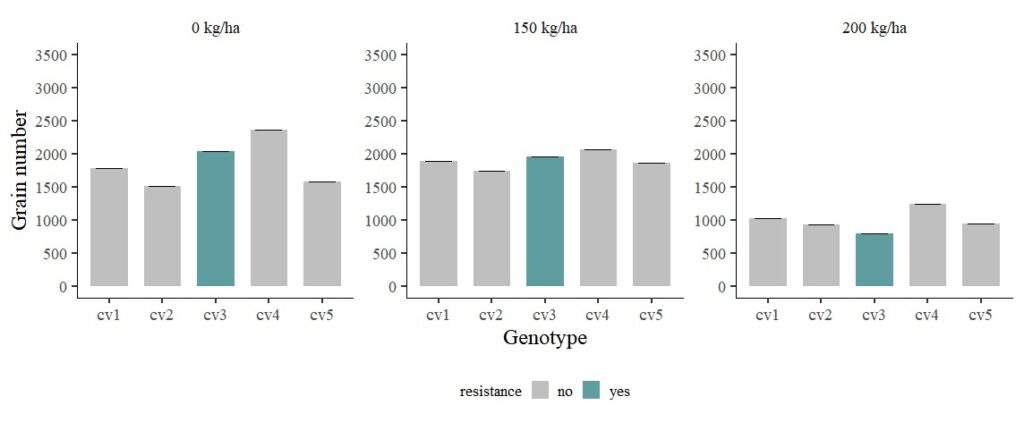
Now, the errors were adjusted by BLUE.
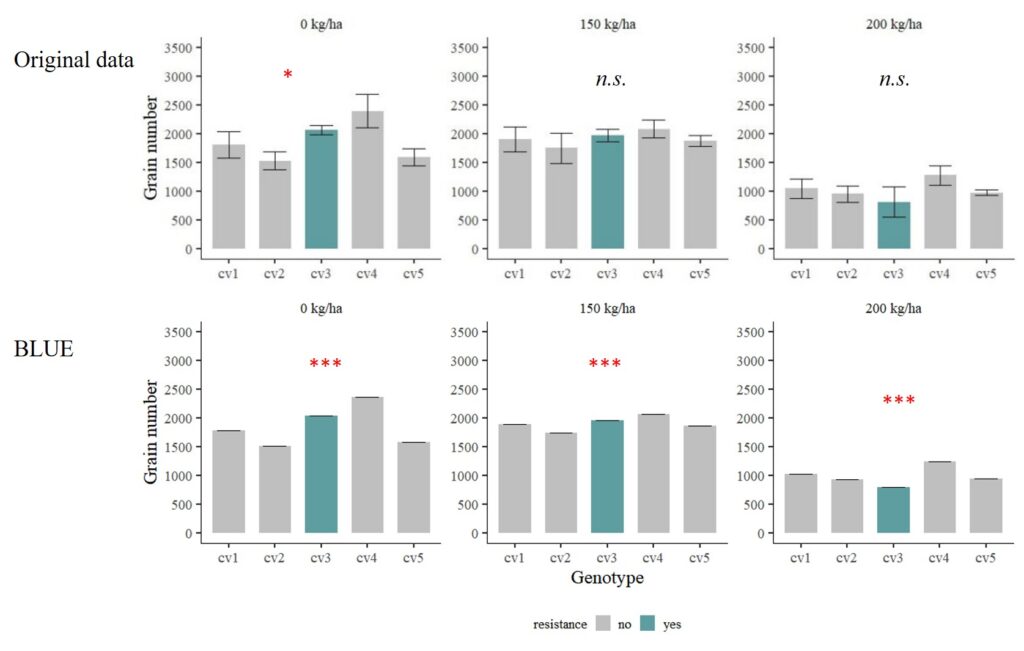
Let’s consider another scenario: cv1 and cv2 are genotypes highly susceptible to disease, while cv4 and cv5 are genotypes less susceptible to disease.
dataB$traits= ifelse(dataB$genotype=="cv1"|dataB$genotype=="cv2", "high susceptible",
ifelse(dataB$genotype=="cv4"|dataB$genotype=="cv5", "less susceptible", "resistance"))
dataB
genotype plot resistance fertilizer GN AGW BLUE_GN traits
1 cv1 1 no 150 1310 33.15 1885.7234 high susceptible
2 cv1 1 no 0 1168 25.07 1783.2109 high susceptible
3 cv1 1 no 200 570 36.04 1020.6757 high susceptible
4 cv2 1 no 150 1120 53.05 1737.2744 high susceptible
5 cv2 1 no 0 1230 26.71 1512.8475 high susceptible
6 cv2 1 no 200 795 37.75 924.7064 high susceptible
7 cv3 1 yes 150 2013 27.51 1951.3979 resistance
8 cv3 1 yes 0 2183 24.61 2042.1957 resistance
9 cv3 1 yes 200 1034 36.53 789.3776 resistance
10 cv4 1 no 150 2451 31.58 2064.1596 less susceptible
.
.
.library(dplyr)
dataC = data.frame(dataB %>%
group_by(traits, resistance, fertilizer) %>%
dplyr::summarize(across(c(GN, BLUE_GN),
.fns= list(Mean=~mean(., na.rm= TRUE),
SD= ~sd(., na.rm= TRUE),
n=~length(.),
se=~sd(.,na.rm= TRUE)/sqrt(length(.))))))
dataC= dataC[,-c(5,6,9,10)]
library (stringr)
dataC$fertilizer= str_replace_all(dataC$fertilizer, '\\b0\\b', '0 kg/ha')
dataC$fertilizer= str_replace_all (dataC$fertilizer, '150','150 kg/ha')
dataC$fertilizer= str_replace_all (dataC$fertilizer, '200','200 kg/ha')
library (ggplot2)
FIG1=ggplot(data=dataC, aes(x=traits, y=BLUE_GN_Mean, fill=resistance))+
geom_bar(stat="identity",position="dodge", width= 0.7, size=1) +
scale_fill_manual(values=c("grey75","cadetblue"))+
geom_errorbar(aes(ymin=BLUE_GN_Mean-BLUE_GN_se, ymax=BLUE_GN_Mean+BLUE_GN_se),
position=position_dodge(0.9), width=0.5) +
scale_y_continuous(breaks=seq(0,3500,500), limits = c(0,3500)) +
facet_wrap (~ fertilizer, scales="free_y") +
labs(x="Genotype", y="Grain number") +
theme_classic(base_size=18, base_family="serif")+
theme(legend.position="bottom",
legend.title=element_text(family="serif", face="plain",
size=13, color= "Black"),
legend.key=element_rect(color="white", fill="white"),
legend.text=element_text(family="serif", face="plain",
size=13, color= "Black"),
legend.background=element_rect(fill="white"),
axis.line=element_line(linewidth=0.5, colour="black"),
strip.background=element_rect(color="white",
linewidth=0.5,linetype="solid"))
FIG1 + windows(width=12, height=5)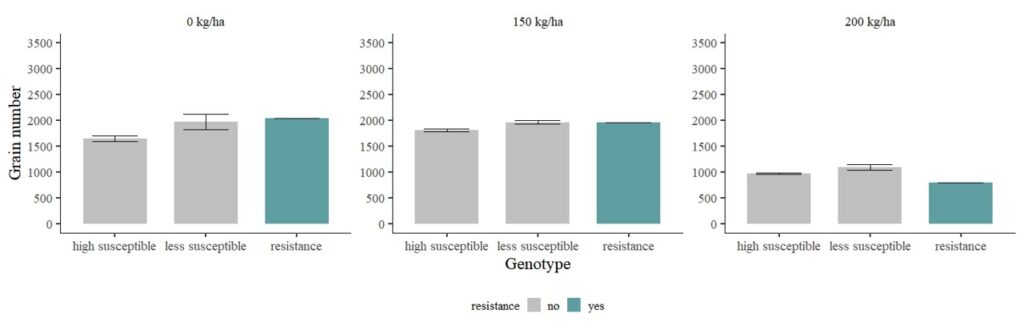
full code; https://github.com/agronomy4future/r_code/blob/main/BLUE_practice
library(readr)
library(lme4)
library(Matrix)
library(dplyr)
library (stringr)
github="https://raw.githubusercontent.com/agronomy4future/raw_data_practice/main/genotype_transgenic_line_with_fertilizer.csv"
dataA= data.frame(read_csv(url(github), show_col_types= FALSE))
dataA= subset(dataA, genotype!="Transgeic_line")
BLUE_0_kg_ha=lmer(GN ~ 0 + (1|genotype), data=subset(dataA, fertilizer=="0"))
BLUE_150_kg_ha=lmer(GN ~ 0 + (1|genotype), data=subset(dataA, fertilizer=="150"))
BLUE_200_kg_ha=lmer(GN ~ 0 + (1|genotype), data=subset(dataA, fertilizer=="200"))
BLUE_0= predict (BLUE_0_kg_ha)
BLUE_150= predict (BLUE_150_kg_ha)
BLUE_200=predict (BLUE_200_kg_ha)
dataA$predicted_0 <- NA
dataA$predicted_0[dataA$fertilizer==0] <- BLUE_0
dataA$predicted_150 <- NA
dataA$predicted_150[dataA$fertilizer==150] <- BLUE_150
dataA$predicted_200 <- NA
dataA$predicted_200[dataA$fertilizer==200] <- BLUE_200
dataB= dataA %>%
mutate(BLUE_GN= coalesce(predicted_0, predicted_150, predicted_200))
dataB= dataB[,-c(7,8,9)]
dataB$traits= ifelse(dataB$genotype=="cv1"|dataB$genotype=="cv2", "+ susceptible",
ifelse(dataB$genotype=="cv4"|dataB$genotype=="cv5", "- susceptible", "resistance"))
dataC = data.frame(dataB %>%
group_by(traits, resistance, fertilizer) %>%
dplyr::summarize(across(c(GN, BLUE_GN),
.fns= list(Mean=~mean(., na.rm= TRUE),
SD= ~sd(., na.rm= TRUE),
n=~length(.),
se=~sd(.,na.rm= TRUE)/sqrt(length(.))))))
dataC$fertilizer= str_replace_all(dataC$fertilizer, '\\b0\\b', '0 kg/ha')
dataC$fertilizer= str_replace_all (dataC$fertilizer, '150','150 kg/ha')
dataC$fertilizer= str_replace_all (dataC$fertilizer, '200','200 kg/ha')
library (ggplot2)
FIG1=ggplot(data=dataC, aes(x=traits, y=BLUE_GN_Mean, fill=resistance))+
geom_bar(stat="identity",position="dodge", width= 0.7, size=1) +
scale_fill_manual(values=c("grey75","cadetblue"))+
geom_errorbar(aes(ymin=BLUE_GN_Mean-BLUE_GN_se, ymax=BLUE_GN_Mean+BLUE_GN_se),
position=position_dodge(0.9), width=0.5) +
scale_y_continuous(breaks=seq(0,3500,500), limits = c(0,3500)) +
facet_wrap (~ fertilizer, scales="free_y") +
labs(x="Genotype", y="Grain number") +
theme_classic(base_size=18, base_family="serif")+
theme(legend.position="bottom",
legend.title=element_text(family="serif", face="plain",
size=13, color= "Black"),
legend.key=element_rect(color="white", fill="white"),
legend.text=element_text(family="serif", face="plain",
size=13, color= "Black"),
legend.background=element_rect(fill="white"),
axis.line=element_line(linewidth=0.5, colour="black"),
strip.background=element_rect(color="white",
linewidth=0.5,linetype="solid"))
FIG1 + windows(width=13, height=5)