What is Finlay-Wilkinson Regression Model?
The genotype is dependent on environmental changes. One genotype may strongly respond to certain environmental conditions, while another genotype may weakly respond to the same conditions. If some genotypes strongly respond under better conditions, they would be adaptable to the environment.
Adaptability refers to the flexibility of a genotype in its response to improved environments.
If a certain genotype exhibits high performance across a wide range of environmental conditions, it would be considered to have broad adaptation.
To achieve this definition, two prerequisites are required.
- In general, greater performances
- Less variation across environmental ranges
I’ll create one dataset.
Env= c("High_inoc","High_NO_inoc","Low_inoc", "Low_NO_inoc")
CV1= c(30,150,20,100)
CV2= c(74,99,49,73)
CV3= c(78,106,56,69)
CV4= c(86,92,66,70)
CV5= c(74,98,57,79)
Data= data.frame(Env,CV1,CV2,CV3,CV4,CV5)
Data
Env CV1 CV2 CV3 CV4 CV5
High_inoc 30 74 78 86 74
High_NO_inoc 150 99 106 92 98
Low_inoc 20 49 56 66 57
Low_NO_inoc 100 73 69 70 79
There are five different genotypes (CV1 – CV5), and each genotype was subjected to four different treatments. Let’s assume that the combination of organic matter and virus inoculation was applied to each genotype to observe the differences in final yield.
High_inoc: High organic matter + virus inoculation
High_NO_inoc: High organic matter + virus free
Low_inoc: Low organic matter + virus inoculation
Low_NO_inoc : Low organic matter + virus free
Which treatment would affect yield the most negatively? Maybe under the low organic matter and inoculation (the worst condition), the yield would be the lowest.
Let’s see it’s true.
library(dplyr)
Data$Mean= rowMeans (Data %>% select(-Env))
Data= rbind(Data, c("Mean", colMeans(Data %>% select(-Env))))
Data
Env CV1 CV2 CV3 CV4 CV5 Mean
High_inoc 30 74 78 86 74 68.4
High_NO_inoc 150 99 106 92 98 109.0
Low_inoc 20 49 56 66 57 49.6
Low_NO_inoc 100 73 69 70 79 78.2
Mean 75.0 73.75 77.25 78.5 77.0 76.3We can calculate two different averages: each genotype across treatments, and each treatment (or environment) across genotypes. As we assumed, the condition of low organic matter and inoculation (Low_inoc) showed the lowest yield (49.6). For genotype, CV4 showed the greatest yield across treatments (78.5).
So, is it okay to say that CV4 is the best cultivar for yield? It would be the best cultivar for yield as it shows the greatest yield across environmental conditions. However, let’s focus on the worst condition (Low_inoc). If CV4 is the best cultivar, it should also show the greatest yield in Low_inoc. However, it seems not because it is 66 in Low_inoc, showing the lowest yield. As mentioned above, the average of Low_inoc was 49.6, and CV4 contributes to the lowest yield in Low_inoc. Therefore, we should not only consider yield but also adaptability when comparing genotypes across different environmental conditions.
Environmental Index will explain adaptability.
Now, I’ll calculate environmental index. This is the difference between the mean of each environment and the grand mean (X.. - X.j).
68.4 – 76.3 = -7.9
109 – 76.3 = 32.7
49.6 – 76.3 = -26.7
78.2 – 76.3 = 1.9
library(dplyr)
Data$Mean= as.numeric(Data$Mean)
Data$Env_index= Data$Mean - Data$Mean[nrow(Data)]
Data
Env CV1 CV2 CV3 CV4 CV5 Mean Env_index
High_inoc 30 74 78 86 74 68.4 -7.9
High_NO_inoc 150 99 106 92 98 109.0 32.7
Low_inoc 20 49 56 66 57 49.6 -26.7
Low_NO_inoc 100 73 69 70 79 78.2 1.9
Mean 75.0 73.75 77.25 78.5 77.0 76.3 0.0I calculated the environmental index for four different environmental conditions. As expected, at Low_inoc (low organic matter + virus inoculation), it shows the lowest environmental index (-26.7). Conversely, at High_NO_inoc (high organic matter + virus-free), it shows the highest environmental index (32.7).
Environmental Index will be independent variable in linear regression.
Now, each genotype will be fitted by linear regression. Of course, yield will be the dependent variable (y). Then, what would be the independent variable (x) in the regression model? In the Finlay-Wilkinson Regression Model, the environmental index becomes the independent variable (x). Therefore, the environmental index should be stacked in rows.
First, I’ll delete the mean I calculated.
Data= Data [-5,-7] # delete 5th row and 7th column
Data
Env CV1 CV2 CV3 CV4 CV5 Env_index
1 High_inoc 30 74 78 86 74 -7.9
2 High_NO_inoc 150 99 106 92 98 32.7
3 Low_inoc 20 49 56 66 57 -26.7
4 Low_NO_inoc 100 73 69 70 79 1.9Then, I’ll stack data in rows using the below code.
library(tidyr)
df= data.frame(
Data %>%
pivot_longer(
cols=c(CV1, CV2, CV3, CV4, CV5),
names_to="Genotype", values_to="Yield")
)
df
Env Env_index Genotype Yield
High_inoc -7.9 CV1 30
High_inoc -7.9 CV2 74
High_inoc -7.9 CV3 78
High_inoc -7.9 CV4 86
High_inoc -7.9 CV5 74
High_NO_inoc 32.7 CV1 150
.
.
.Now I’ll fit each genotype with an environmental index using the code below.
if(!require(dplyr)) install.packages("dplyr")
library(dplyr)
summary(lm (Yield ~ Env_index, data=dataA %>% filter (Genotype=="CV1")))
summary(lm (Yield ~ Env_index, data=dataA %>% filter (Genotype=="CV2")))
summary(lm (Yield ~ Env_index, data=dataA %>% filter (Genotype=="CV3")))
summary(lm (Yield ~ Env_index, data=dataA %>% filter (Genotype=="CV4")))
summary(lm (Yield ~ Env_index, data=dataA %>% filter (Genotype=="CV5")))or
regression= dataA%>% group_by(Genotype) %>% do(model= lm(Yield~Env_index, data=.))
regression$model
[[1]]
Call:
lm(formula = Yield ~ Env_index, data = .)
Coefficients:
(Intercept) Env_index
75.00 2.34
[[2]]
Call:
lm(formula = Yield ~ Env_index, data = .)
Coefficients:
(Intercept) Env_index
73.7500 0.8025
[[3]]
Call:
lm(formula = Yield ~ Env_index, data = .)
Coefficients:
(Intercept) Env_index
77.250 0.804
[[4]]
Call:
lm(formula = Yield ~ Env_index, data = .)
Coefficients:
(Intercept) Env_index
78.5000 0.3786
[[5]]
Call:
lm(formula = Yield ~ Env_index, data = .)
Coefficients:
(Intercept) Env_index
77.0000 0.6754 However, I recommend using the following code.
if(!require(broom)) install.packages("broom")
library(broom)
regression1= df %>% group_by(Genotype) %>% do(tidy(lm(Yield ~ Env_index, data=.)))
regression1
Genotype term estimate std.error statistic p.value
CV1 (Intercept) 75.0000000 12.1638994 6.165786 0.025309723
CV1 Env_index 2.3395736 0.5658852 4.134361 0.053823885
CV2 (Intercept) 73.7500000 2.7528814 26.790112 0.001390415
CV2 Env_index 0.8024564 0.1280687 6.265828 0.024537235
CV3 (Intercept) 77.2500000 4.3607461 17.714859 0.003171427
CV3 Env_index 0.8039714 0.2028693 3.963002 0.058171978
CV4 (Intercept) 78.5000000 5.0252942 15.620976 0.004073090
CV4 Env_index 0.3786387 0.2337852 1.619601 0.246746749
CV5 (Intercept) 77.0000000 1.1734503 65.618456 0.000232165
CV5 Env_index 0.6753598 0.0545909 12.371290 0.006470516Now, let’s focus on the slope of the regression in each genotype. Which genotype shows the steepest slope? It’s CV1 (2.34).
The model equation of CV1 is y = 75.0 + 2.317 * Env_Index. This means that when the environmental index increases by 1, yield will increase by 2.317 times.
For a clearer visualization, I’ll draw a regression graph.
library(ggplot2)
ggplot(data=df, aes(x=as.numeric(Env_index), y=as.numeric(Yield), group=Genotype)) +
geom_smooth(method = lm, level=0.95, se=FALSE, linetype=1, color="Dark red",
linewidth=0.5, formula= y ~ x) +
geom_point (aes(shape=Genotype, fill=Genotype), col="Black", size=5, stroke = 0.5) +
scale_shape_manual(values = c(21, 22, 23, 24, 25)) +
scale_fill_manual(values = c("Black","Red",'Blue',"Orange","Green")) +
scale_x_continuous(breaks = seq(-40,40,10), limits = c(-40,40)) +
scale_y_continuous(breaks = seq(0,200,20), limits = c(0,200)) +
labs(x="Environmental Index", y="Yield") +
theme_classic(base_size=18, base_family="serif")+
theme(legend.position=c(0.89,0.17),
legend.title=element_blank(),
legend.key=element_rect(color="white", fill="white"),
legend.text=element_text(family="serif", face="plain",
size=15, color= "Black"),
legend.background=element_rect(fill="white"),
axis.line=element_line(linewidth=0.5, colour="black"))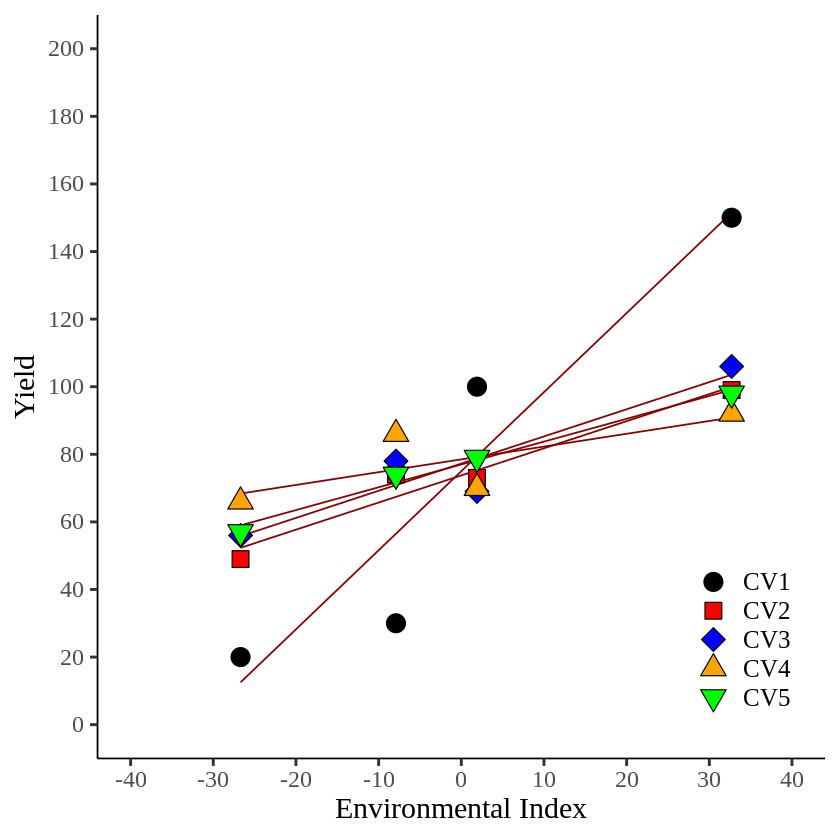
Now it’s much clear. CV1 shows the steepest slope among genotypes. If we consider only yield across environmental conditions, CV4 showed the greatest yield, but it shows less slope than CV1.
CV1: y=75.0 + 2.317 * Env_Index
CV4: y=78.5 + 0.374 * Env_Index
Therefore, in terms of adaptability, we might be able to say CV4 is the best cultivar. That is, in Finlay-Wilkinson Regression Model, CV4 would have the greatest environmental adaptability.
full code: https://github.com/agronomy4future/r_code/blob/main/What_is_Finlay_Wilkinson_Regression_Model.ipynb
The model equation of Finlay-Wilkinson regression
p = G + βE + e where G is intercept (genotypic effect) β is slope (sensitivity to environment; adaptability)) e is error
In this post, I explained how to obtain β.
When we analyze our field data across environmental conditions, β would provide many more insights about our crops. Particularly, when we analyze genotypes under multi-environmental trials (METs), the Finlay-Wilkinson regression would be very useful to understand how genotypes respond to environments.
■ fwrmodel() package
Github: https://github.com/agronomy4future/fwrmodel
To easily calculate the environmental index, I recently developed an R package called fwrmodel(). I will use the same data mentioned above to calculate the environmental index.
Env= c("High_inoc","High_NO_inoc","Low_inoc", "Low_NO_inoc")
CV1= c(30,150,20,100)
CV2= c(74,99,49,73)
CV3= c(78,106,56,69)
CV4= c(86,92,66,70)
CV5= c(74,98,57,79)
Data= data.frame(Env,CV1,CV2,CV3,CV4,CV5)
Env CV1 CV2 CV3 CV4 CV5
High_inoc 30 74 78 86 74
High_NO_inoc 150 99 106 92 98
Low_inoc 20 49 56 66 57
Low_NO_inoc 100 73 69 70 79First, we need to transpose the dataset as shown below
if(!require(dplyr)) install.packages("dplyr")
if(!require(tidyr)) install.packages("tidyr")
library(dplyr)
library(tidyr)
dataA= data.frame(Data %>%
pivot_longer(
cols= c(CV1,CV2,CV3,CV4,CV5),
names_to= "Cultivar",
values_to= "Yield"))
dataA
Env Cultivar Yield
1 High_inoc CV1 30
2 High_inoc CV2 74
3 High_inoc CV3 78
4 High_inoc CV4 86
5 High_inoc CV5 74
6 High_NO_inoc CV1 150
7 High_NO_inoc CV2 99
8 High_NO_inoc CV3 106
9 High_NO_inoc CV4 92
10 High_NO_inoc CV5 98
11 Low_inoc CV1 20
12 Low_inoc CV2 49
13 Low_inoc CV3 56
14 Low_inoc CV4 66
15 Low_inoc CV5 57
16 Low_NO_inoc CV1 100
17 Low_NO_inoc CV2 73
18 Low_NO_inoc CV3 69
19 Low_NO_inoc CV4 70
20 Low_NO_inoc CV5 79I’ll calculate the environmental index for each cultivar in relation to the environment using the fwrmodel() package.
# installation
if(!require(remotes)) install.packages("remotes")
remotes::install_github("agronomy4future/fwrmodel")
library(remotes)
library(fwrmodel)
stability= fwrmodel(df, env_cols = c("Env"),
genotype_col= "Cultivar", yield_cols= c("Yield"))
env_index_cal= data.frame(stability$env_index)
env_index_cal
Cultivar Env Environments Env_index_Yield Yield
1 CV1 High_inoc High_inoc -7.9 30
2 CV2 High_inoc High_inoc -7.9 74
3 CV3 High_inoc High_inoc -7.9 78
4 CV4 High_inoc High_inoc -7.9 86
5 CV5 High_inoc High_inoc -7.9 74
6 CV1 High_NO_inoc High_NO_inoc 32.7 150
7 CV2 High_NO_inoc High_NO_inoc 32.7 99
8 CV3 High_NO_inoc High_NO_inoc 32.7 106
9 CV4 High_NO_inoc High_NO_inoc 32.7 92
10 CV5 High_NO_inoc High_NO_inoc 32.7 98
11 CV1 Low_inoc Low_inoc -26.7 20
12 CV2 Low_inoc Low_inoc -26.7 49
13 CV3 Low_inoc Low_inoc -26.7 56
14 CV4 Low_inoc Low_inoc -26.7 66
15 CV5 Low_inoc Low_inoc -26.7 57
16 CV1 Low_NO_inoc Low_NO_inoc 1.9 100
17 CV2 Low_NO_inoc Low_NO_inoc 1.9 73
18 CV3 Low_NO_inoc Low_NO_inoc 1.9 69
19 CV4 Low_NO_inoc Low_NO_inoc 1.9 70
20 CV5 Low_NO_inoc Low_NO_inoc 1.9 79and let’s obtain slope (stability).
coefficient_AGW= as.data.frame(stability$regression$Yield)
coefficient_AGW
Cultivar term estimate std.error statistic p.value
1 CV1 (Intercept) 75.0000000 12.1638994 6.165786 0.025309723
2 CV1 Env_index_Yield 2.3395736 0.5658852 4.134361 0.053823885
3 CV2 (Intercept) 73.7500000 2.7528814 26.790112 0.001390415
4 CV2 Env_index_Yield 0.8024564 0.1280687 6.265828 0.024537235
5 CV3 (Intercept) 77.2500000 4.3607461 17.714859 0.003171427
6 CV3 Env_index_Yield 0.8039714 0.2028693 3.963002 0.058171978
7 CV4 (Intercept) 78.5000000 5.0252942 15.620976 0.004073090
8 CV4 Env_index_Yield 0.3786387 0.2337852 1.619601 0.246746749
9 CV5 (Intercept) 77.0000000 1.1734503 65.618456 0.000232165
10 CV5 Env_index_Yield 0.6753598 0.0545909 12.371290 0.006470516■ [R package] Finlay-Wilkinson Regression model (feat. fwrmodel)
