[R package] Finlay-Wilkinson Regression model (feat. fwrmodel)
■ What is Finlay-Wilkinson Regression Model?
In my previous post, I introduced what Finlay-Wilkinson Regression Model is and how to calculate adaptability (or stability). Actually, adaptability and stability are opposite concept with the same data. Have you ever heard heritability (h2)? Heritability is a key concept in genetics and breeding that measures how much of the variation in a trait within a population is due to genetic differences among individuals. In other words, it quantifies the proportion of phenotypic variation (observable traits) that can be attributed to genetic factors.
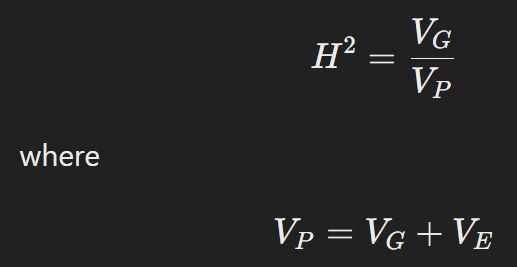
High Heritability means that a large portion of the trait’s variation is due to genetic differences, suggesting that the trait is more stable and less influenced by environmental factors. This implies that the trait is less plastic, or less responsive to changes in the environment. On the other hand, low heritability indicates that environmental factors play a larger role in the variation of the trait. Traits with low heritability are more plastic, meaning they show greater variability in response to different environmental conditions.
Adaptability and stability are analogous to the inverse relationship between heritability and plasticity.
Adaptability refers to a trait’s ability to change or respond effectively to different environmental conditions. A trait with high adaptability will show significant variation in response to environmental changes. For instance, a crop variety with high adaptability may perform well across a wide range of environments, but its performance might vary significantly depending on the conditions. High adaptability generally means a trait has greater plasticity, or flexibility, to respond to environmental changes. This can be beneficial in environments that are highly variable but may come with trade-offs in terms of consistency.
On the other hand, stability reflects how consistent a trait’s performance is across varying environments. A trait with high stability will show little variation in response to different environmental conditions, indicating that it performs reliably regardless of changes in the environment. High stability indicates that a trait performs consistently across different environments, but it might not show as much variation or responsiveness to environmental changes. This can be advantageous for ensuring reliable performance but may not be as flexible in adapting to new or extreme conditions.
Therefore, the concepts of adaptability and stability are indeed complementary but inversely related: improving one can often come at the expense of the other. Understanding this trade-off is crucial in fields like crop breeding, where both adaptability and stability might be desired but need to be balanced according to specific goals and environmental contexts.
■ Quantifying Phenotypic Plasticity of Crops
To calculate adaptability or stability (hereafter referred to as stability), the first step is to calculate the environmental index.
if(!require(dplyr)) install.packages("dplyr")
library(dplyr)
Condition= c("High_inoc", "High_NO_inoc", "Low_inoc", "Low_NO_inoc")
CV= matrix(c(30, 74, 78, 86, 74, 150, 99, 106, 92, 98, 20, 49, 56, 66, 57, 100, 73, 69, 70, 79), ncol= 5, byrow= TRUE)
colnames(CV)= paste0("CV", 1:5)
df= data.frame(Condition, CV)
df$Mean= rowMeans (df %>% select(-Condition))
df= rbind(df, c("Mean", colMeans(df %>% select(-Condition))))
Env CV1 CV2 CV3 CV4 CV5 Mean
High_inoc 30 74 78 86 74 68.4
High_NO_inoc 150 99 106 92 98 109.0
Low_inoc 20 49 56 66 57 49.6
Low_NO_inoc 100 73 69 70 79 78.2
Mean 75.0 73.75 77.25 78.5 77.0 76.3
df$Mean= as.numeric(df$Mean)
df$Env_index= df$Mean - df$Mean[nrow(df)]
Env CV1 CV2 CV3 CV4 CV5 Mean Env_index
High_inoc 30 74 78 86 74 68.4 -7.9
High_NO_inoc 150 99 106 92 98 109.0 32.7
Low_inoc 20 49 56 66 57 49.6 -26.7
Low_NO_inoc 100 73 69 70 79 78.2 1.9
Mean 75.0 73.75 77.25 78.5 77.0 76.3 0.0The code provided outlines the general process for calculating the environmental index. However, most datasets we work with will not follow the structure shown above. I combined two variables—nitrogen (high or low) and virus (inoculated or non-inoculated)—into a single factor and displayed the genotypes (CV1 to CV5) horizontally. In an actual dataset, the structure would be more like the example below.
Nitrogen Virus Genotype Yield
High inoc CV1 30
High inoc CV2 74
High inoc CV3 78
High inoc CV4 86
High inoc CV5 74
High noinoc CV1 150
High noinoc CV2 99
High noinoc CV3 106
High noinoc CV4 92
High noinoc CV5 98
Low inoc CV1 20
Low inoc CV2 49
Low inoc CV3 56
Low inoc CV4 66
Low inoc CV5 57
Low noinoc CV1 100
Low noinoc CV2 73
Low noinoc CV3 69
Low noinoc CV4 70
High noinoc CV5 79In this case, we need to reorganize the dataset and calculate the environmental index step by step.
■ fwrmodel() package
To solve this program, recently I developed R package to calculate environmental index and stability simultaneously. It’s fwrmodel() package.
Github: https://github.com/agronomy4future/fwrmodel
Let’s upload one dataset.
if(!require(readr)) install.packages("readr")
library(readr)
github="https://raw.githubusercontent.com/agronomy4future/raw_data_practice/main/fwrm_package_data_practice.csv"
df= data.frame(read_csv(url(github), show_col_types=FALSE))
set.seed(100)
df[sample(nrow(df),5),]
year variety nitrogen location AGW KN GY
202 2023 cv2 N0 Nebraska 318.6 3764 11864.8
112 2024 cv2 N1 Iowa 313.6 4570 14177.8
206 2023 cv2 N0 Nebraska 338.9 3764 12619.8
4 2023 cv1 N1 Iowa 311.7 3476 10721.4
98 2024 cv1 N1 Iowa 263.9 5618 14669.2
.
.
.Let’s assume this data represents grain weight (AGW), grain number per m² (KN), and grain yield (kg/ha, GY) of corn across different states in the U.S. for two different seasons. I want to calculate the stability of each yield component and grain yield to determine which genotypes show better stability for AGW, KN, and GY, respectively.
First, I’ll install the package, but before that, it’s necessary to install Rtools because my package was developed outside of CRAN.
https://cran.r-project.org/bin/windows/Rtools

Please install the version corresponding to your current R version, and install the fwrmodel() package as the following code.
if(!require(remotes)) install.packages("remotes")
remotes::install_github("agronomy4future/fwrmodel")
library(remotes)
library(fwrmodel)and I’ll run the code as shown below to calculate the environmental index.
stability= fwrmodel(df, env_cols = c("year", "nitrogen", "location"),
genotype_col= "variety", yield_cols= c("AGW","GY","KN"))
env_index_cal= data.frame(stability$env_index)set.seed(100)
env_index_cal[sample(nrow(env_index_cal),5),]
variety year nitrogen location Environments Env_index_AGW AGW Env_index_GY GY Env_index_KN KN
20170 cv2 2023 N0 Nebraska 2023_N0_Nebraska 3.443333 318.6 -435.7763 11810.8 -214.5600 3488
16887 cv1 2023 N0 Illinois 2023_N0_Illinois -1.523333 307.0 -2300.4197 8130.4 -786.9267 2742
3430 cv2 2023 N1 Iowa 2023_N1_Iowa -22.023333 337.4 -202.7063 11931.9 195.4400 3721
3696 cv2 2023 N1 Iowa 2023_N1_Iowa -22.023333 289.0 -202.7063 10474.6 195.4400 3411
20474 cv2 2023 N0 Nebraska 2023_N0_Nebraska 3.443333 348.8 -435.7763 10947.9 -214.5600 3672I want to calculate the environmental index for AGW, KN, and GY across year, nitrogen, and location, respectively. The code to do this is as shown above.
Note 1
Setting up environments to calculate environmental index is important because it directly affects stability (slope). For example, if you think the year is not an important factor for crop yield in this case, you might combine environments with only nitrogen and location. This could result in a completely different slope for each genotype. Therefore, the most important thing is to understand your own dataset and determine the best combination of environments to calculate stability.
Next, I’ll calculate stability.
coefficient_AGW= as.data.frame(stability$regression$AGW)
coefficient_KN= as.data.frame(stability$regression$KN)
coefficient_GY= as.data.frame(stability$regression$GY)Let’s check the coefficient for AGW.
print(coefficient_AGW)
variety term estimate std.error statistic p.value
1 cv1 (Intercept) 297.9520000 3.95194803 75.393704 1.368777e-88
2 cv1 Env_index_AGW 0.7523172 0.14292608 5.263681 8.336224e-07
3 cv2 (Intercept) 318.8220000 2.58702388 123.238909 2.795793e-109
4 cv2 Env_index_AGW 0.8862399 0.09356226 9.472194 1.693111e-15
5 cv3 (Intercept) 312.6860000 2.64794053 118.086489 1.787034e-107
6 cv3 Env_index_AGW 1.3614429 0.09576537 14.216443 1.487695e-25The slope represents stability: a flatter slope indicates greater stability across environments, while a steeper slope suggests less stability. In this data, cv1 show better stability.
Let’s visualize this!!
if(!require(dplyr)) install.packages("dplyr")
library(dplyr)
if(!require(ggplot2)) install.packages("ggplot2")
library(ggplot2)
data_summary= data.frame(env_index_cal %>%
group_by(Environments, variety) %>%
dplyr::summarize(across(c(AGW, Env_index_AGW),
.fns = list(Mean = mean,
n = length))))
ggplot(data=data_summary, aes(x=Env_index_AGW_Mean, y=AGW_Mean))+
geom_smooth(aes(group=variety, color=variety), method='lm', linetype=1, se=FALSE,
formula=y~x, linewidth=0.5)+
geom_point(aes(fill=variety, shape=variety), color="black", size=4)+
scale_color_manual(values=c("grey15","grey35","grey75"))+
scale_fill_manual(values=c("grey15","grey35","grey75"))+
scale_shape_manual(values=c(21,22,23))+
scale_x_continuous(breaks=seq(-50,50,25), limits=c(-50,50))+
scale_y_continuous(breaks=seq(200,400,50), limits=c(200,400))+
labs(x="Environmental_Index", y="Average grain weight (mg)") +
theme_classic(base_size=20, base_family="serif")+
theme(legend.position=c(0.89,0.13),
legend.title=element_blank(),
legend.key=element_rect(color=alpha("white",.001),
fill=alpha("white",.001)),
legend.background=element_rect(fill=alpha("white",.001)),
panel.grid.major= element_line(color="grey90", linetype="dashed"),
axis.line=element_line(linewidth=0.5, colour="black"))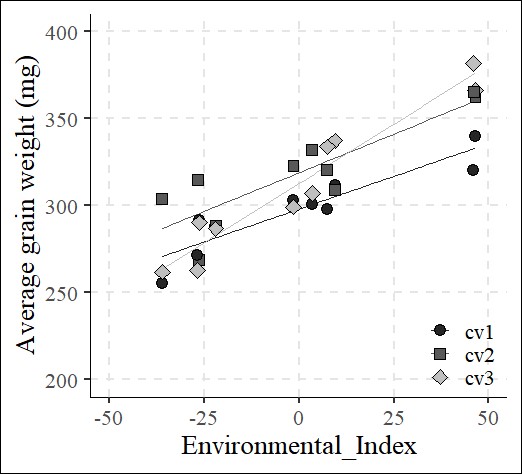
The slope of cv1 is the flattest, while cv3 is the steepest among three genotypes, as indicated by the coefficient_AGW. Therefore, cv1 shows the most stability for grain weight, whereas cv3 is more variable or plastic across environments.
□ code summary: https://github.com/agronomy4future/r_code/blob/main/R_package__fwrmodel.ipynb
