[STAT Article] Steps to Calculate Log-Likelihood Prior to AIC and BIC: [Part 2] ANOVA model

In my previous post, I explained how to calculate the Log-Likelihood, AIC, and BIC in a regression model. In this post, I will demonstrate the same concepts, but in the context of an ANOVA model.
Here I have one dataset.
if(!require(readr)) install.packages("readr")
library(readr)
github="https://raw.githubusercontent.com/agronomy4future/raw_data_practice/refs/heads/main/Fertilizer%20(One%20Way%20ANOVA).csv"
df= data.frame(read_csv(url(github), show_col_types=FALSE))
head(df[sample(nrow(df), 10), ])
Fertilizer Yield
9 Control 12.4
19 Slow 16.0
5 Control 11.8
17 Slow 15.8
7 Control 13.1
24 Fast 8.8
.
.
.Let’s say this data represents yield in response to different fertilizer types (Control, Slow, and Fast), and I want to determine the effect of fertilizer type on yield. Therefore, I will perform a one-way ANOVA.
model= aov(Yield~ Fertilizer, data=df)
summary(model)
Df Sum Sq Mean Sq F value Pr(>F)
Fertilizer 2 207.68 103.84 394.3 <2e-16 ***
Residuals 27 7.11 0.26 Now, I observe that the effect of fertilizer on yield is significant. Next, I will calculate the Log-Likelihood, AIC, and BIC for this one-way ANOVA. The equation for the Log-Likelihood in ANOVA is shown below. It may seem tricky at first, but once you understand the principle, it becomes a piece of cake.
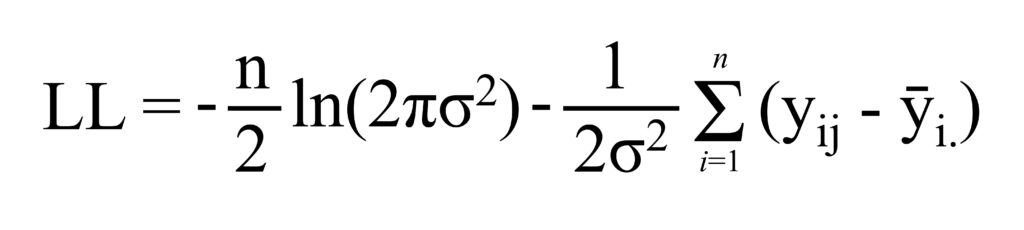
Reading my previous post would be helpful for understanding the process of these calculations.
In this dataset, there is one factor, which is fertilizer, and the replicates were not designated as blocks. Therefore, this is a one-way ANOVA without blocks. In other words, it follows a Completely Randomized Design (CRD).
The model equation is as follows:
yij= μ + τi + ϵij
Where:
yij = yield for fertilizer treatment 𝑖 and replicate 𝑗
μ = grand mean of yield
τi = Effect of fertilizer treatment 𝑖
εij = Residual error for the observation at treatment 𝑖 and replicate 𝑗
Based on this model equation, I will analyze the variation in the data.
| x | yij | ȳ.. | ȳi. | ȳi. – ȳ.. | yij – ȳi. | yij – ȳ.. | (ȳi. – ȳ..)2 | (yij – ȳi.)2 | (yij – ȳ..)2 |
| Fertilizer | Yield | Grand mean | Fertilizer mean | Fertilizer effect | Residuals | Total | Fertilizer effect^2 | Residuals^2 | Total^2 |
| Control | 12.2 | 12.46 | 12.13 | -0.33 | 0.07 | -0.26 | 0.11 | 0.00 | 0.07 |
| Control | 12.4 | 12.46 | 12.13 | -0.33 | 0.27 | -0.06 | 0.11 | 0.07 | 0.00 |
| Control | 11.9 | 12.46 | 12.13 | -0.33 | -0.23 | -0.56 | 0.11 | 0.05 | 0.31 |
| Control | 11.3 | 12.46 | 12.13 | -0.33 | -0.83 | -1.16 | 0.11 | 0.69 | 1.34 |
| Control | 11.8 | 12.46 | 12.13 | -0.33 | -0.33 | -0.66 | 0.11 | 0.11 | 0.43 |
| Control | 12.1 | 12.46 | 12.13 | -0.33 | -0.03 | -0.36 | 0.11 | 0.00 | 0.13 |
| Control | 13.1 | 12.46 | 12.13 | -0.33 | 0.97 | 0.64 | 0.11 | 0.94 | 0.41 |
| Control | 12.7 | 12.46 | 12.13 | -0.33 | 0.57 | 0.24 | 0.11 | 0.32 | 0.06 |
| Control | 12.4 | 12.46 | 12.13 | -0.33 | 0.27 | -0.06 | 0.11 | 0.07 | 0.00 |
| Control | 11.4 | 12.46 | 12.13 | -0.33 | -0.73 | -1.06 | 0.11 | 0.53 | 1.12 |
| Slow | 16.6 | 12.46 | 15.83 | 3.37 | 0.77 | 4.14 | 11.38 | 0.59 | 17.17 |
| Slow | 15.8 | 12.46 | 15.83 | 3.37 | -0.03 | 3.34 | 11.38 | 0.00 | 11.18 |
| Slow | 16.5 | 12.46 | 15.83 | 3.37 | 0.67 | 4.04 | 11.38 | 0.45 | 16.35 |
| Slow | 15.0 | 12.46 | 15.83 | 3.37 | -0.83 | 2.54 | 11.38 | 0.69 | 6.47 |
| Slow | 15.4 | 12.46 | 15.83 | 3.37 | -0.43 | 2.94 | 11.38 | 0.18 | 8.66 |
| Slow | 15.6 | 12.46 | 15.83 | 3.37 | -0.23 | 3.14 | 11.38 | 0.05 | 9.88 |
| Slow | 15.8 | 12.46 | 15.83 | 3.37 | -0.03 | 3.34 | 11.38 | 0.00 | 11.18 |
| Slow | 15.8 | 12.46 | 15.83 | 3.37 | -0.03 | 3.34 | 11.38 | 0.00 | 11.18 |
| Slow | 16.0 | 12.46 | 15.83 | 3.37 | 0.17 | 3.54 | 11.38 | 0.03 | 12.56 |
| Slow | 15.8 | 12.46 | 15.83 | 3.37 | -0.03 | 3.34 | 11.38 | 0.00 | 11.18 |
| Fast | 9.5 | 12.46 | 9.4 | -3.05 | 0.09 | -2.96 | 9.28 | 0.01 | 8.74 |
| Fast | 9.5 | 12.46 | 9.4 | -3.05 | 0.09 | -2.96 | 9.28 | 0.01 | 8.74 |
| Fast | 9.6 | 12.46 | 9.4 | -3.05 | 0.19 | -2.86 | 9.28 | 0.04 | 8.16 |
| Fast | 8.8 | 12.46 | 9.4 | -3.05 | -0.61 | -3.66 | 9.28 | 0.37 | 13.37 |
| Fast | 9.5 | 12.46 | 9.4 | -3.05 | 0.09 | -2.96 | 9.28 | 0.01 | 8.74 |
| Fast | 9.8 | 12.46 | 9.4 | -3.05 | 0.39 | -2.66 | 9.28 | 0.15 | 7.06 |
| Fast | 9.1 | 12.46 | 9.4 | -3.05 | -0.31 | -3.36 | 9.28 | 0.10 | 11.27 |
| Fast | 10.3 | 12.46 | 9.4 | -3.05 | 0.89 | -2.16 | 9.28 | 0.79 | 4.65 |
| Fast | 9.5 | 12.46 | 9.4 | -3.05 | 0.09 | -2.96 | 9.28 | 0.01 | 8.74 |
| Fast | 8.5 | 12.46 | 9.4 | -3.05 | -0.91 | -3.96 | 9.28 | 0.83 | 15.66 |
| Σ | 207.68 | 7.11 | 214.79 |
Reading my previous post would be helpful for understanding the process of these calculations.
■ Understanding Mean Absolute Error (MAE) in ANOVA: A Step-by-Step Guide to Calculation in Excel
If you can understand the equation of the Log-Likelihood, you can see the equation as follows:

I already calculate Sum of Squared Error (SSE), which is 7.11, and I’ll calculate Mean Squared Error (MSE) by dividing degree of freedom (n – t) where n is total sample number and t is the number of levels in the factor, which n is 30, and t is 27 (= 30 – 3 as there are 3 fertilizer types)
However, when calculating MSE for the Log-Likelihood, it is calculated as SSE/n, not SSE/(n-t)
Therefore, MSE is 7.11 / 30 ≈ 0.237
Now, it’s a piece of the cake to calculate the Log-Likelihood
LL = (-30/2)*ln(2*3.14*0.237) - (1/(2*0.237))*7.11
≈ -20.97
The Log-Likelihood for this ANOVA model is around -20.97
Let’s verify this value is correct using R.
First, you can easily find SSE and MSE in the ANOVA table.
model= aov(Yield~ Fertilizer, data=df)
summary(model)
Df Sum Sq Mean Sq F value Pr(>F)
Fertilizer 2 207.68 103.84 394.3 <2e-16 ***
Residuals 27 7.11 0.26 The ANOVA table provide SSE value as 7.11, but MSE is calculated as SSE/(n-t), which is 7.11 / 27 (=30-3) ≈ 0.26, but as mentioned, for the Log-Likelihood, MSE will be calculated as 7.11/30 ≈ 0.237
To calculate the Log-Likelihood, R provides a simple code.
logLik(model)
'log Lik.' -20.97484 (df=4)You can see the same value as what we calculate by hand. Therefore, we can verify the calculation for Log-Likelihood is correct.
df=4 correspond to one intercept parameter, two regression coefficients for the levels of the Fertilizer variable (with one level used as the reference category), and one variance parameter for the residuals.
Let’s understand how to calculate the Log-Likelihood manually. We’ll calculate it step by step in R, not simply using logLik(model).
residuals= resid(model)
SSE=sum(residuals^2)
MSE= SSE / length(df$Yield)
LL= -length(df$Yield)/2*(log(2*pi*MSE)) - SSE/(2*MSE)
cat("Log-likelihood:", LL, "\n")
Log-likelihood: -20.97484 Then, now we can calculate Akaike information criterion (AIC) and Bayesian Information Criterion (BIC).
The Akaike Information Criterion (AIC) is a statistical measure used to compare and evaluate different models based on their goodness of fit and complexity. It helps to identify the model that best balances fit (how well the model explains the data) and complexity (how many parameters the model uses).
The formula for AIC:
AIC= 2*k - 2*ln(L)
where:
k is the number of parameters in the model
ln(L) is the likelihood of the model
We already calculated Log-Likelihood, and k is 4 in the model. Also, given this, the number of parameters, k used in the AIC formula is 4
Therefore, AIC is calculated as 2*4 - 2*-20.97 = 49.94
let’s verify this value is correct using R.
AIC (model)
49.94968My calculation is correct!!
Let’s calculate BIC. The Bayesian Information Criterion (BIC) is another model selection criterion, similar to the Akaike Information Criterion (AIC), but it applies a stronger penalty for models with more parameters. The goal of BIC, like AIC, is to balance model fit (how well the model explains the data) with model complexity (how many parameters the model uses).
The formula for BIC:
BIC= k*ln(n) - 2*ln(L)
where:
k is the number of parameters in the model
ln(L) is the likelihood of the model
n is the number of data points.
Again, we already calculated Log-Likelihood, and k is 4 in the model. Also, given this, the number of parameters, k used in the BIC formula is 4.
Therefore, AIC is calculated as 4*ln(30) - (2*-20.97) = 55.55
let’s verify this value is correct using R.
BIC (model)
55.55447My calculation is correct!!
How about more factors are added?
The One-Way ANOVA model is the simplest model, but we’ll have more factors in the experimental fields. Let’s discuss again with another dataset.
Cultivar= rep(c("CV1","CV2"),each=12)
Nitrogen= rep(rep(c("N0","N1","N2","N3"), each=3),2)
Block= rep(c("I","II","III"),8)
Yield= c (99, 109, 89, 115, 142, 133, 121, 157, 142, 125, 150, 139, 82, 104, 99, 117, 125, 127, 145, 154, 154, 151, 166, 175)
df= data.frame(Cultivar,Nitrogen,Block,Yield)
head(df[sample(nrow(df), 10), ])
Cultivar Nitrogen Block Yield
13 CV2 N0 I 82
17 CV2 N1 II 125
16 CV2 N1 I 117
18 CV2 N1 III 127
8 CV1 N2 II 157
21 CV2 N2 III 154
.
.
.In this case, we want to analyze how yield is affected by nitrogen fertilizer across different genotypes. Both genotype and fertilizer would be treated as factors, while replicates are considered blocks, indicating a Randomized Complete Block Design (RCBD).
If you want to calculate the variation in the data for this Two-Way ANOVA with blocks in Excel, reading my previous post could help you understand the process behind these calculations.
■ Easy-to-Understand Guide to Factorial Experiments and Two-Way ANOVA
Now, I’ll analyze two-way ANOVA using R.
model= aov(Yield~ Cultivar+Nitrogen+Cultivar:Nitrogen+ factor(Block), data=df)
summary(model)
Df Sum Sq Mean Sq F value Pr(>F)
Cultivar 1 253 253 4.99 0.042327 *
Nitrogen 3 10695 3565 70.17 1.12e-08 ***
factor(Block) 2 1505 752 14.81 0.000351 ***
Cultivar:Nitrogen 3 1040 347 6.82 0.004604 **
Residuals 14 711 51 In this ANOVA table, you can find SSE, and calculate MSE. SSE is 711, and MSE will be 711/24 = 29.625
Then, we can calculate the Log-Likelihood
LL = (-24/2)*ln(2*3.14*29.625) - (1/(2*29.625))*711
≈ -74.72
The Log-Likelihood for this ANOVA model is around -74.71186. Let’s verify this value is correct using R.
logLik(model)
'log Lik.' -74.72217 (df=11)df = 11 correspond to the following: one intercept parameter, one regression coefficient for the levels of the genotype variable (Cultivar, with one level used as the reference category), three regression coefficients for the levels of the nitrogen variable (Nitrogen, with one level used as the reference category), two regression coefficients for the levels of the block variable (Block, with one level used as the reference category), three regression coefficients for the interaction between the genotype and nitrogen variables (1 for the genotype × 3 for nitrogen, excluding reference levels), and one parameter for the residual variance.
Total Parameters:
1(Intercept)+1(Genotype)+3(Nitrogen)+2(Block)+3(Interaction)+1(Residual Variance)= 11
Again, let’s calculate manually using R.
residuals= resid(model)
SSE=sum(residuals^2)
MSE= SSE / length(df$Yield)
LL= -length(df$Yield)/2*(log(2*pi*MSE)) - SSE/(2*MSE)
cat("Log-likelihood:", LL, "\n")
Log-likelihood: -74.72217 My calculation is correct. Let’s calculate AIC and BIC.
AIC= 2*k - 2*ln(L) = 2*11 - 2*-74.72217
= 171.4443
BIC= k*ln(n) - 2*ln(L) = 11*ln(24) - 2*-74.72217
= 184.4029
Using R, I’ll check my calculation is correct.
AIC (model)
171.4443
BIC (model)
184.4029From, now on you can calculate the Log-Likelihood, AIC and BIC when you see the ANOVA table.

We aim to develop open-source code for agronomy (kimjk@agronomy4future.com)